The Seven Bridges of Königsberg problem

The Seven Bridges of Königsberg problem is a famous puzzle in mathematics that originated in the 18th century. The city of Königsberg (now known as Kaliningrad, Russia) was situated on the Pregel River and included two large islands connected and the mainland by seven bridges. The challenge was to find a walk through the city that would cross each bridge exactly once and return to the starting point.
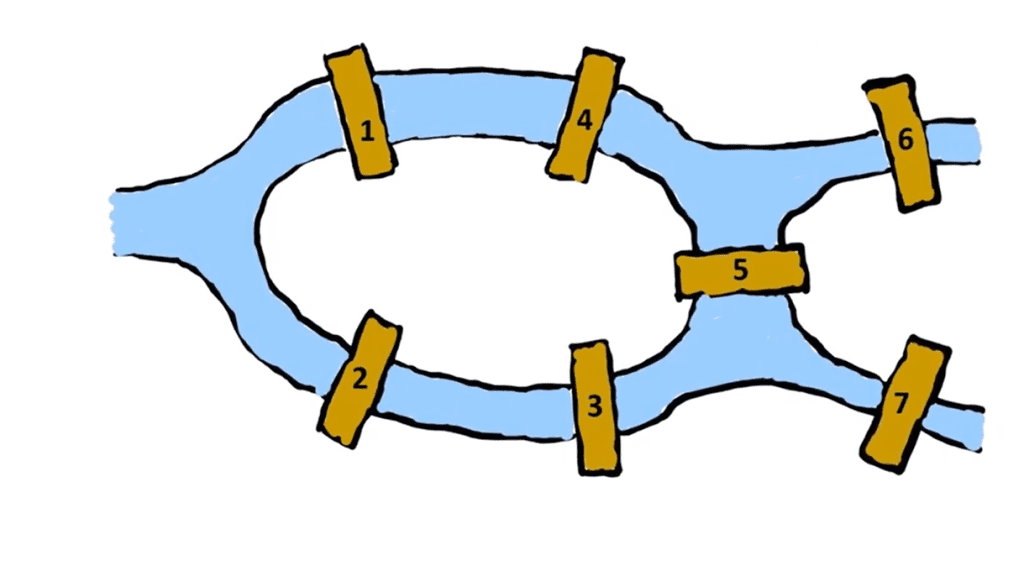
The problem was first introduced by the Swiss mathematician Leonhard Euler in 1736. Euler simplified the city’s layout by representing the landmasses as points and the bridges as lines connecting them. He then formulated the problem as a graph theory question, now known as the Eulerian path or circuit problem.
Euler’s solution demonstrated that finding a walk that crossed each bridge only once and returned to the starting point was impossible. He proved that for such a walk to exist, each landmass (or “node” in graph theory) would need an even number of bridges connected. However, in the case of Königsberg, there were four nodes with an odd number of bridges, making it an unsolvable problem.
Euler’s work on the Seven Bridges of Königsberg problem laid the foundation for graph theory, which has since become a fundamental branch of mathematics with applications in various fields, including computer science, transportation planning, and network analysis.
The solution